Two equivalent though apparently non-related problems

In the framework of maintenance decision-making, a subject addressed by the DIGEST Project, reliability refers to the probability that a certain device will be functional without failure.

If the time between failures of the device follows a random variable, one random variable of interest that emerges in reliability theory is the remaining time until the next failure of a device given a time horizon. This variable is known as the residual life of the device in stochastic processes theory.

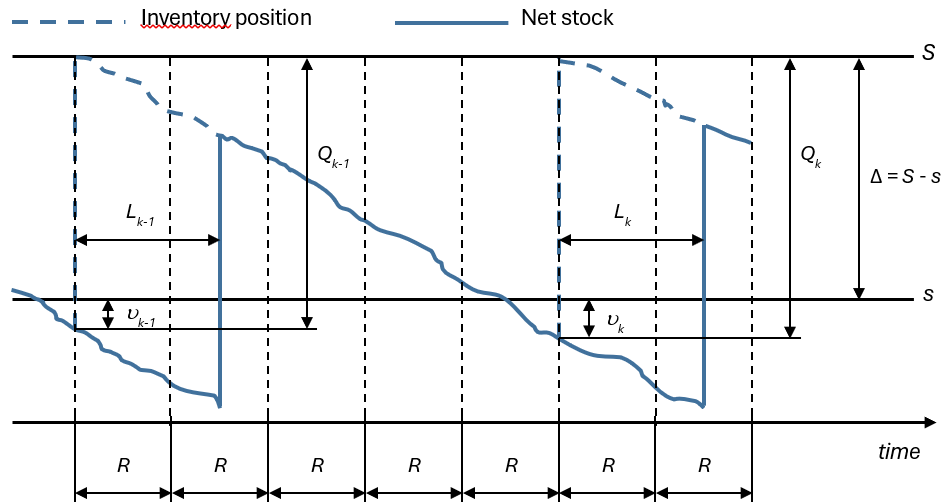
This variable is also of significant interest in other stochastic processes of a fundamentally different nature, such as those arising in inventory systems studied within inventory theory. In the so-called reorder point, order-up-to-level inventory systems, stock is withdrawn from the warehouse to fulfill demands following a random variable. When the inventory position—defined as the stock on-hand plus stock on-order minus backorders— is at or below the reorder point, an order is placed so that the inventory position rises to the order-up-to level. When the reorder point is crossed, and a replenishment order is triggered, the difference between the reorder point and the inventory position is known as the undershoot.

Although in inventory systems the undershoot refers to a quantity and not an interval, the undershoot random variable also corresponds to the residual life as defined in stochastic processes theory.

Under the framework of a research Project preceding the current DIGEST Project, Gutierrez and Rivera (2021) developed the first analytical expression of the residual life, including a computationally tractable expression for the case of gamma distributed time between failures or demands in a reorder point, order-up-to-level inventory system.